卷积 (Convolution)

离散形式： $[P_X*P_Y](s) = \sum\limits_{x=1}^{N}P_X(x)\cdot{P}_Y(s-x)$

连续形式： $[f*g](s) = \int_{-\infty}^{\infty}f(x)g(s-x)dx$

如何理解卷积？

卷积是一种将两个数组或函数结合起来的方法。卷积时，对两个函数自变量取关于 $s$ 对称的 $x1$ , $x2$ , 即确保自变量之和相同。主要关注 $x$ 的物理意义：

当函数为 概率密度函数 时，自变量 $x$ 表示取的某个值，而因变量 $y$ 表示值为 $x$ 时的概率密度，在确保 $x_1+x_2=s$ , 即所有的 $x$ 组合之和均相同时，此时 $f\cdot{g}$ 表示当前组合下的概率密度，而卷积 $f*g$ 则表示构成和为 $s$ 的所有组合的概率密度总和，即在分布 $f$ , $g$ 中分别抽样后之和为 $s$ 的 新分布的概率密度。

当函数为 输入信号函数 与 单位冲激函数 时， $x$ 值表示时间 $t$ ，当两函数对应时间之和相同时，表示从 $0$ 到 $t$ 时刻所有的的信号与单位冲激函数的组合，并且满足时间关系。例如：信号函数取 $T=t$ 时，单位冲激函数取 $T=0$ ，而信号函数取 $T=t-1$ 时，单位冲激函数取 $T=1$ ，即在 $t$ 时刻， $t-1$ 处的信号对应的系统响应。故卷积表示在某时刻 $t$ 下，之前所有时刻系统响应的累加。

在图形中，卷积的某个点 $s$ 对应的值为两个函数 $f$ , $g$ 对应点的乘积所构成的新图形所围成的面积

convolution_vis

正态分布

当对同一个分布不断地进行卷积，即对其不断地采样，采样结果的最终分布会逼近正态分布。

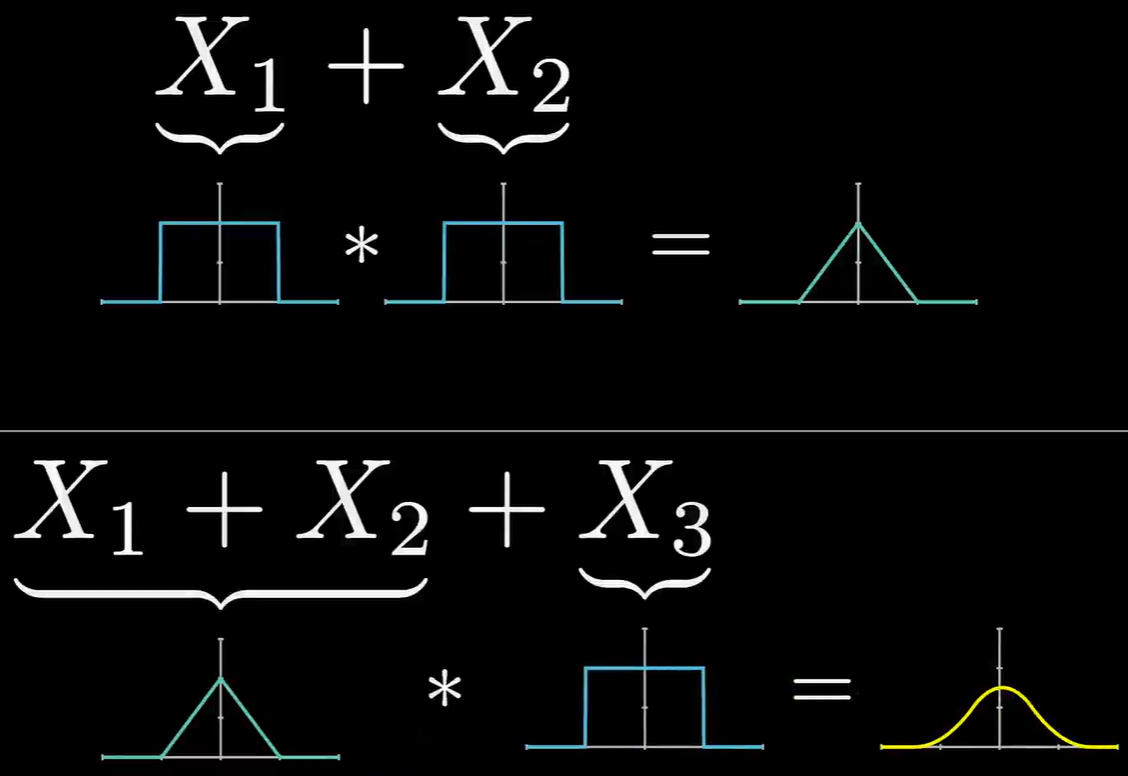
normal_dist

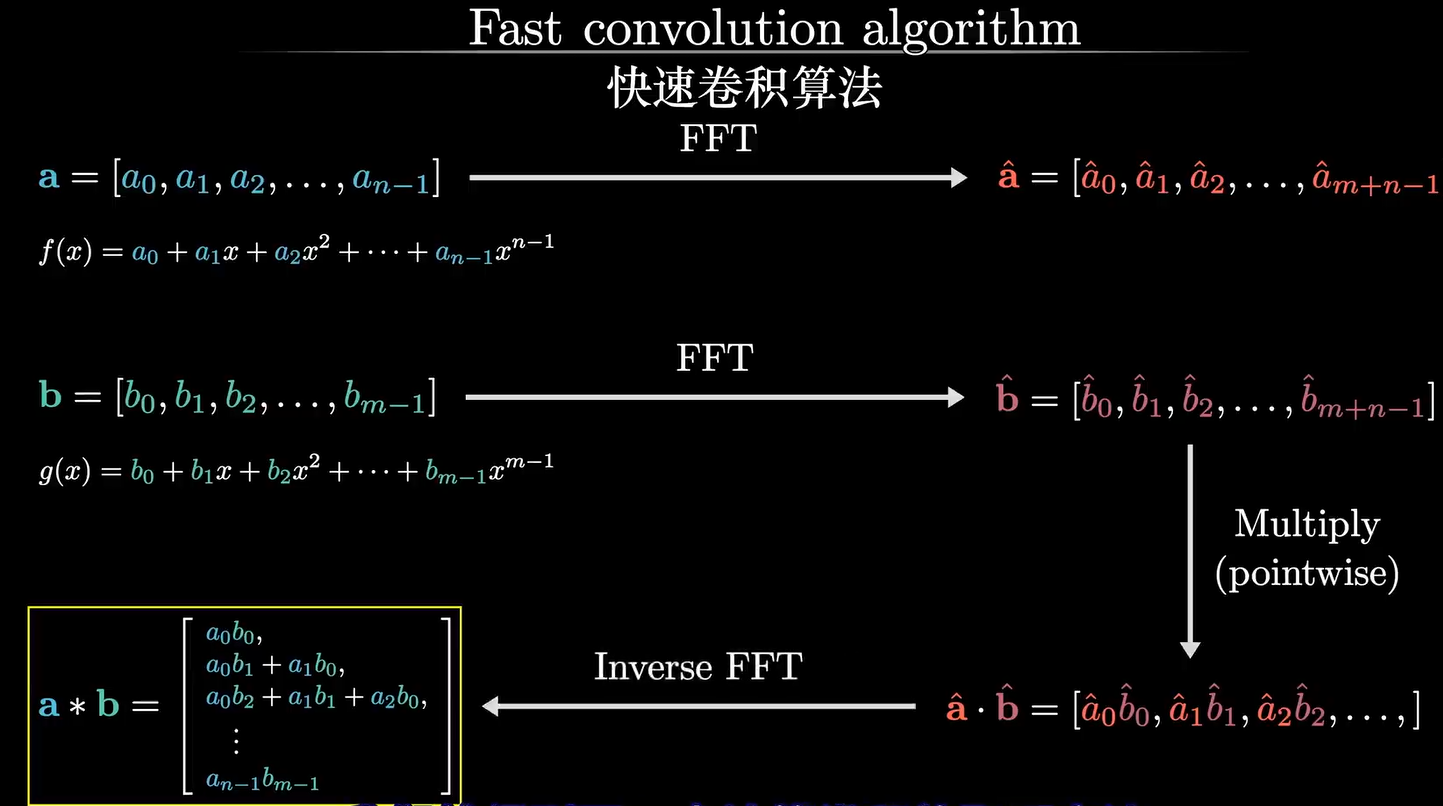
快速求卷积 (FFT)

可以通过快速傅里叶变换，将卷积计算的复杂度从 $O(N^2)$ 降低至 $O(Nlog(N))$

fast_convolution_algo

参考

3Blue1Brown 视频

卷积 (Convolution)

如何理解卷积？​

正态分布​

快速求卷积 (FFT)​

参考​

如何理解卷积？

正态分布

快速求卷积 (FFT)

参考